Trees

In this tutorial, we’ll be covering Binary Trees, Binary Search Trees, and K-ary Trees. We will review some common terminology that is shared amongst all of the trees and then dive into specifics of the different types.

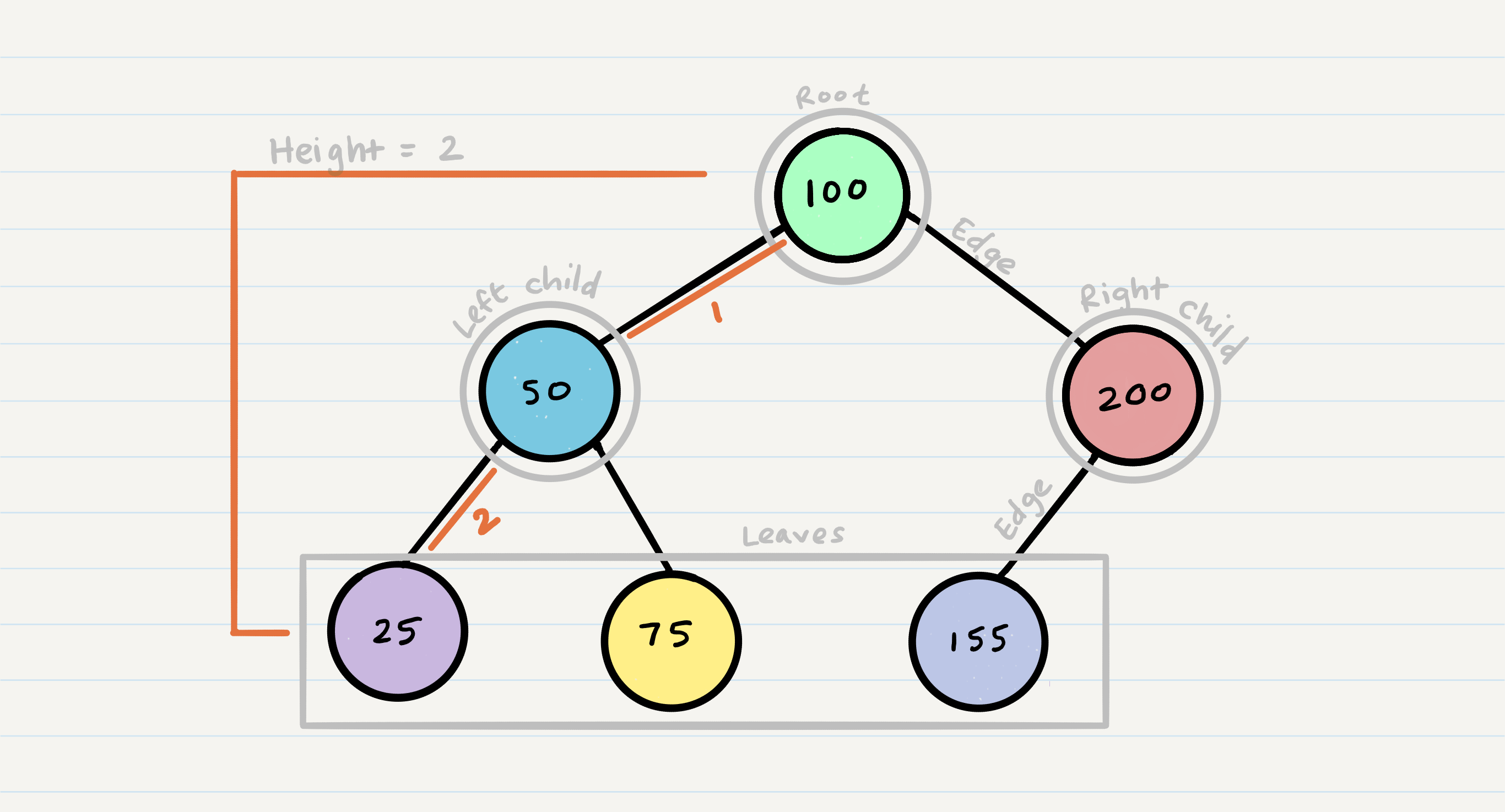
Common Terminology

1. Node - A Tree node is a component which may contain it’s own values, and references to other nodes
2. Root - The root is the node at the beginning of the tree
3. K - A number that specifies the maximum number of children any node may have in a k-ary tree. In a binary tree, k = 2.
4. Left - A reference to one child node, in a binary tree
5. Right - A reference to the other child node, in a binary tree
6. Edge - The edge in a tree is the link between a parent and child node
7. Leaf - A leaf is a node that does not have any children
8. Height - The height of a tree is the number of edges from the root to the furthest leaf

Sample Tree

Traversals

An important aspect of trees is how to traverse them. Traversing a tree allows us to search for a node, print out the contents of a tree, and much more! There are two categories of traversals when it comes to trees:

1. Depth First
2. Breadth First

Depth First

Depth first traversal is where we prioritize going through the depth (height) of the tree first. There are multiple ways to carry out depth first traversal, and each method changes the order in which we search/print the root. Here are three methods for depth first traversal:

• Pre-order: root » left » right
• In-order: left » root » right
• Post-order: left » right » root

Breadth First

Breadth first traversal iterates through the tree by going through each level of the tree node-by-node.

Traditionally, breadth first traversal uses a queue (instead of the call stack via recursion) to traverse the width/breadth of the tree.